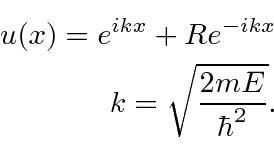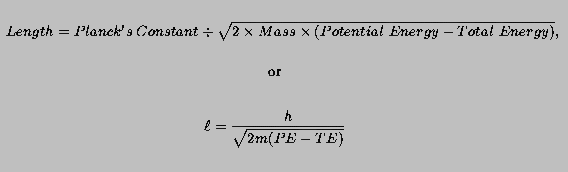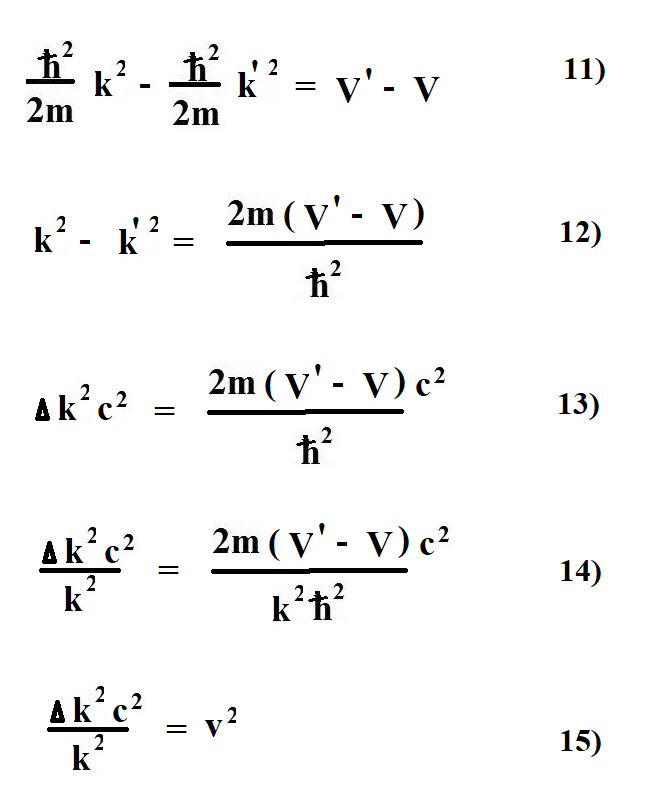The Definition of Universal Momentum Operator of Quantum Mechanics and the Essence of Micro-Particle's Spin——To Reveal the Real Reason That the Bell Inequality Is Not Supported by Experiments
The Hamiltonian in Quantum Mechanics
The Potential Step
Relativistic Kinetic Energy (Integration By Parts)
Hamiltonians and Quantum Mechanics - ppt download
Lecture 3 wavefunctions and probability Quantum mechanics describes
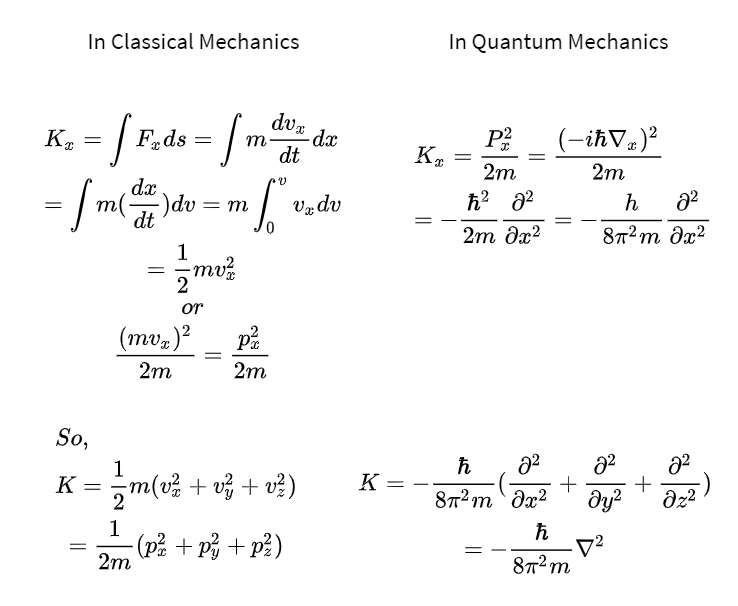
quantum mechanics - Trouble understanding method used in the proof of Kinetic Energy operator is Hermitian - Physics Stack Exchange
SOLVED:In quantum mechanics, the momentum operator in the T direction is ih 0 pI 2t d1 and the kinetic energy operator for one-dimensional particle is h2 22 T = 812m D12 Show
Solved In quantum mechanics, the momentum operator in the x | Chegg.com
Solved Problems Quantum Physics - Engineering Physics Class
Energy Calculation for Rigid Rotor Molecules
Introduction to Quantum Theory - ppt video online download
6. Rotational energies. In classical mechanics, the | Chegg.com
The Hamiltonian Operator - Quantum Chemistry - PSIBERG
Visual Quantum Mechanics
Atomic physics Part PHYS261
Hamiltonian (quantum mechanics) - Wikipedia
GM Jackson Physics and Mathematics: Deriving Newton's Constant G From Quantum Physics
Hamiltonian (quantum mechanics) - Wikipedia
Chapter 3 Quantum Mechanics In physics, ei(kr
The Hamiltonian Operator - Quantum Chemistry - PSIBERG
Solved David Griffiths, Introduction to Quantum Mechanics | Chegg.com
What is a Hamiltonian Operator?
